6. Various types of binary diagrams in relation to the nature of interactions w
6.1 Weakly interacting systems with total solid miscibility
Figure 4 shows a simple system where the two components are miscible in all proportions in both the liquid phase L and the solid solution α. Only two phases occupy the equilibrium diagram. At high temperatures, the L phase and, at low temperatures, the α phase. Isomorphic pure bodies A* and B* melt at 900 and 700°C respectively. Between these two temperatures, the diagram shows two conjugate liquid and solid lines called liquidus and solidus forming a spindle of phase coexistence that closes at the ends of the diagram on the two melting points of the pure bodies. The two regular interactions are...
The Ultimate Scientific and Technical Reference
This article is included in
Studies and properties of metals
This offer includes:
Knowledge Base
Updated and enriched with articles validated by our scientific committees
Services
A set of exclusive tools to complement the resources
Practical Path
Operational and didactic, to guarantee the acquisition of transversal skills
Doc & Quiz
Interactive articles with quizzes, for constructive reading
Various types of binary diagrams in relation to the nature of interactions w
Solidification and segregation coefficient
Diagram classification
In this folder, the diagrams are arranged in alphabetical order of the symbol of the element concerned, which comes first in alphabetical order among the elements making up the alloy; then, for a given element, in alphabetical order of the symbol of the second element.
Example
we find Fe-C to C-Fe.
...
Binary alloys containing Ag
Binary alloys containing Al
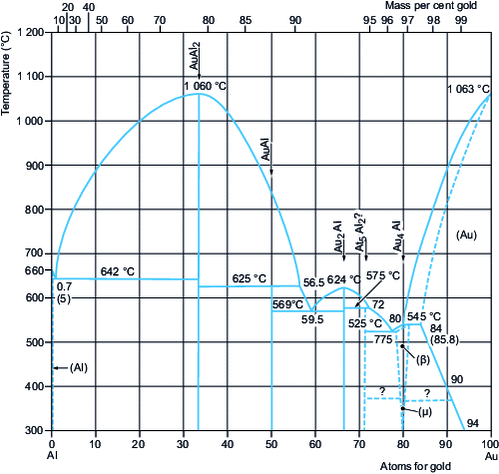
Binary alloys containing As
As-Cu (arsenic-copper – figure )
This diagram has recently been completely revised. The relationships between phases and their compositions are now well known; there are apparently no other intermediate phases richer in arsenic than those shown in the diagram.
-
Phase structures
(Cu) : c. f. c....
Au-containing binary alloys
Binary alloys containing either B, Be or Bi
Binary alloys containing C
Binary alloys containing either Ca, Cd or Ce
Binary alloys containing Co
Binary alloys containing Cr
Binary alloys containing Cu
Binary alloys containing Fe
Binary alloys containing Li, Mg or Mn
Binary alloys containing either Mo, or N, or Nb, or Ni, or O
Binary alloys containing either Pb, Sb, Sn or Ti
The Ultimate Scientific and Technical Reference
