Présentation
Auteur(s)
-
Bernard DEMOULIN : Docteur ès Sciences Physiques - Maître de Conférences à l’Université des Sciences et Techniques de Lille - Laboratoire de Radiopropagation et Électronique, URA CNRS n 289
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
De nombreux phénomènes physiques, ainsi que la plupart des chaînes de mesure, mettent en jeu des variables aléatoires qui dépendent d’un paramètre déterministe.
Ces processus particuliers appartiennent à la classe des fonctions aléatoires, dont l’exemple le plus concret est représenté par les signaux où le paramètre déterministe n’est autre que la variable temps. Les fonctions aléatoires jouissent de propriétés remarquables qui en simplifient souvent l’étude et la caractérisation. La propriété la plus usuelle est la stationnarité puisqu’elle consiste à reconnaître une quasi-invariance du comportement statistique de la variable aléatoire quelle que soit la valeur attribuée au paramètre déterministe 1. Autrement dit, un signal aléatoire est stationnaire si les moments et la densité de probabilité sont indépendants du temps. Une étude plus attentive des fonctions aléatoires montre cependant que la stationnarité n’est pas toujours acquise et qu’il faut parfois distinguer la stationnarité au sens strict de celle qui regarde l’ordre des moments de la fonction.
Une autre propriété, étroitement associée à la précédente, s’appelle l’ergodisme 2. L’ergodisme apporte d’intéressantes simplifications dans la mesure où l’on peut exploiter la convergence existant entre les moments de la variable aléatoire et les valeurs moyennes de la fonction calculées par intégration sur le paramètre déterministe. Cette propriété n’est pas très aisée à justifier sur le plan théorique, aussi faut-il souvent user de considérations intuitives pour la découvrir.
Le domaine d’application le plus répandu des fonctions aléatoires est certainement le traitement des signaux. Même doté des propriétés de stationnarité et d’ergodicité, un signal aléatoire n’est pas facile à caractériser à cause de l’impossibilité de le décrire analytiquement et d’y associer un spectre au sens habituel de l’intégrale de Fourier.
Les fonctions de corrélation et les densités spectrales de puissance vont toutefois apporter une réponse positive à ce problème.
En effet, les premières sont la généralisation des coefficients de corrélation traitant de systèmes à deux variables aléatoires. On distinguera la fonction d’autocorrélation, dont le principe est d’exprimer la dépendance stochastique de deux échantillons d’un même signal en fonction du décalage temporel qui les sépare, et la fonction d’intercorrélation qui concerne les échantillons de deux signaux distincts 3.
Les exemples montrent qu’il est souvent possible d’exprimer analytiquement ces fonctions et d’accéder ainsi à une représentation mathématique caractérisant les propriétés stochastiques des signaux aléatoires.
Les fonctions d’autocorrélation et d’intercorrélation étant bornées, on peut leur appliquer l’intégrale de Fourier dont le résultat s’appelle l’autospectre et l’interspectre. Cette transformation mathématique, plus connue sous le nom de théorème de Wiener-Khintchine, se révèle un artifice très puissant pour caractériser la signature spectrale des signaux aléatoires stationnaires 4.
Une classe particulière de fonctions aléatoires obéit aux processus de Markov et plus particulièrement aux processus de Gauss-Markov. Nous en rappellerons les principales hypothèses et insisterons sur les propriétés remarquables de leurs fonctions d’autocorrélation 5.
Cet article fait suite à l’article Processus aléatoires Processus aléatoires du présent traité, auquel le lecteur se reportera.
VERSIONS
- Version courante de mars 2014 par Bernard DEMOULIN
DOI (Digital Object Identifier)
Présentation
Article inclus dans l'offre
"Instrumentation et méthodes de mesure"
(50 articles)
Actualisée et enrichie d’articles validés par nos comités scientifiques.
Quiz, médias, tableaux, formules, vidéos, etc.
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses.
Un ensemble de services exclusifs en complément des ressources.
4. Densité spectrale de puissance
4.1 Densité spectrale de puissance des fonctions déterministes
Considérons une fonction déterministe x (t ) bornée ; on peut associer à cette fonction sa duale X (f ) que l’on appelle spectre. Le passage de x (t ) à X (f ) s’obtient par application de la transformée de Fourier directe (notée TF) ; lorsque t est la variable temps, f est une fréquence :
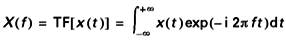
S’il s’agit d’une fonction périodique de période T, X (f ) est un spectre de raies que l’on peut représenter par la relation :
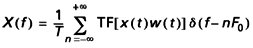
avec δ fonction de Dirac,
expression dans laquelle w (t ) est une fenêtre rectangulaire de largeur T centrée sur l’origine :
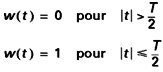
F0 représente la fréquence fondamentale telle que :
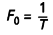
On appelle densité spectrale de puissance de la fonction x (t ) le produit du spectre et de son conjugué. La densité spectrale de puissance sera notée S (f ) :
Lorsque l’unité représentant la variable x contenue dans la fonction bornée x (t ) est U, l’unité de la densité spectrale de puissance est U2Hz–2, à condition toutefois que la variable t soit exprimée en secondes et f en hertz. S’agissant d’une fonction périodique,...
Densité spectrale de puissance
Article inclus dans l'offre
"Instrumentation et méthodes de mesure"
(50 articles)
Actualisée et enrichie d’articles validés par nos comités scientifiques.
Quiz, médias, tableaux, formules, vidéos, etc.
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses.
Un ensemble de services exclusifs en complément des ressources.
Article inclus dans l'offre
"Instrumentation et méthodes de mesure"
(50 articles)
Actualisée et enrichie d’articles validés par nos comités scientifiques.
Quiz, médias, tableaux, formules, vidéos, etc.
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses.
Un ensemble de services exclusifs en complément des ressources.











