Introduction aux propriétés des lois de probabilité

L’observation d’un échantillon d’effectif important du lancer d’un dé a permis d’observer une loi empirique (c’est-à-dire construite à partir d’observations expérimentales) spécifique. En divisant l’effectif de chaque classe par le nombre total de valeurs de l’échantillon, l’histogramme se présente en fréquence (cf. figure Exemple d’histogramme).

Exemple d’histogramme

Chaque fréquence peut être assimilée à une probabilité d’obtenir l’une ou l’autre des valeurs de l’échantillon.

Dans cette représentation en pourcentage, la surface de chaque « bâton » est exprimée en pourcentage de la surface totale. Il s’agit d’une « normalisation » de l’histogramme qui permet d’obtenir une somme de toutes les surfaces égale à 100 %. Cette représentation se nomme Loi de probabilité empirique parce qu’elle représente la répartition de probabilité obtenue à partir d’un échantillon.

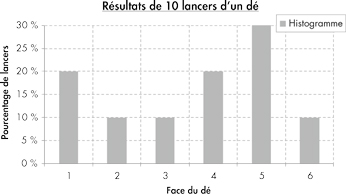
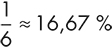Cette loi de probabilité empirique est une approximation de la loi de probabilité théorique du phénomène étudié qui, pour un dé non pipé, est donnée par l’histogramme où chaque « bâton » a pour ordonnée . Il s’agit de la loi dite uniforme discrète. Autrement dit, à chaque lancer du dé, la probabilité théorique d’obtenir l’une des faces vaut la même probabilité (il s’agit d’une situation dite d’équiprobabilité). Chaque lancer du dé peut alors se concevoir comme un « tirage aléatoire » selon cette loi de probabilité théorique.

Lorsque nous étudions un phénomène continu que l’on peut considérer équiprobable sur un intervalle, la loi de probabilité théorique qui le représente est une loi dite uniforme continue représentée par un rectangle. Par exemple, lorsqu’un instrument de mesure est équipé d’un affichage numérique, ce dernier ne peut afficher que des valeurs discrètes : 10,01 ; 10,02 ; 10,03 pour un appareil au 1/100. Ainsi, lorsqu’il affiche 10,02, la valeur réelle est en réalité entre le point où il bascule de 10,01 à 10,02 et celui où il basculera de 10,02 à 10,03. La loi de probabilité de cette erreur est typiquement une loi de probabilité uniforme continue (cf. figure Exemple de loi de probabilité « uniforme »).

Exemple de loi de probabilité « uniforme »

Loi discrète

La loi discrète est une loi dont les valeurs de son support peuvent être décomptées.

Exemple : Le dé produit 6 valeurs distinctes : 1, 2, 3, 4, 5 ou 6. Une pièce qui est lancée offre 2 opportunités pour son résultat : pile ou face

Loi continue

Une loi continue est une loi dont les valeurs de son support se trouvent sur un intervalle (éventuellement infini) de nombres réels.

Exemple : la température de l’eau liquide à la pression atmosphérique peut prendre toutes les valeurs réelles possibles entre 0 °C (Point de glace) et 100 °C (Point de fusion)

Dans le cas de la loi discrète de lancer d’un dé, la probabilité de faire un 1 ou un 6 est égale à la somme des « bâtons » des classes 1 et 6, soit . La probabilité de faire un 1 et un 6 est évidemment nulle puisque le lancer d’un dé ne peut pas produire deux résultats simultanés. Pou...

Il existe une infinité de lois de probabilité. Par exemple, si l’on somme les résultats de  dés (variable d’intérêt) et que l’on s’intéresse à la répartition des valeurs théoriquement attendues, il s’agit de « sommer » lois uniformes discrètes. Cette opération n’est pas sim...

L’hypothèse d’un phénomène suivant une loi normale est très souvent utilisée, au moins en première approximation. Il existe différents tests statistiques pour confirmer (ou infirmer) l’a priori normale pour la loi parente d’un échantillon (cf. section « aller plus loin »). Les proprié...

Comme nous l’avons vu, un échantillon ne représente pas la réalité et il est peu probable de trouver, dans un échantillon, les valeurs limites d’un phénomène. En revanche, les quelques données présentes dans un échantillon permettent d’estimer une valeur pour l‘écart-type de la population parente et...