Présentation
Auteur(s)
-
Jean-Michel POU : Président Fondateur de la société Delta Mu
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleMOTS-CLÉS
Moyenne | écart type | variance | dispersion | capabilité processus | processus | tolérances | spécifications | aptitude | Cp | Cpk | ISO 22514
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Métier : responsable qualité
(254 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Vous mettez en œuvre un procédé de fabrication pour élaborer un produit. Ledit procédé subit en permanence des conditions qui varient, ce qui entraîne des variations dans les caractéristiques du produit final. Par ailleurs, il ne vous est pas possible de mesurer tous les produits réalisés pour assurer la conformité de chacun. La science statistique permet, quant à elle, de quantifier, sur la base de quelques échantillons, la variation totale de la production afin de garantir qu’elle répond, pour tous les produits (ou presque) à l’exigence du client. Cette fiche introduit les concepts nécessaires à cette évaluation qui consiste à vérifier ce que nous nommons « l’aptitude du procédé » ou « capabilité du procédé ».
La vérification de l’aptitude (capabilité) du procédé de fabrication permet au fournisseur de s’assurer de sa propre capacité à satisfaire son client et, par conséquent, de ne s’engager vis-à-vis d’un client que sur des spécifications compatibles avec ses capacités réelles de production.
Étapes :
- 1 - Quelles bases statistiques essentielles pour comprendre les indicateurs d’aptitude ?
- 2 - Quid des indicateurs de la capabilité ?
- 3 - Quid de la capabilité des processus de mesure
- 4 - Échantillonnage
- 5 - Analyse de normalité
- 6 - Court Terme / Long Terme : prenez en compte tous les facteurs de dispersion du procédé
Cet article fait partie de l’offre
Métier : responsable qualité
(254 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Fiche
Fiches à lire
Aller plus loin
Auteur
Jean-Michel Pou
Norme de référence
ISO 22514-7 : Méthodes statistiques dans la gestion de processus - Aptitude et performance - Partie 7 : Aptitude des processus de mesure
Cet article fait partie de l’offre
Métier : responsable qualité
(254 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Annexes









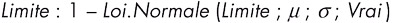
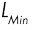 et
et 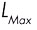 :
: 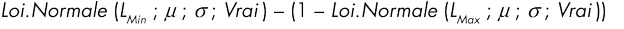 .
.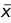 de µ et l’estimation s de σ. La qualité (matérialisée par la largeur de l’intervalle de confiance autour de
de µ et l’estimation s de σ. La qualité (matérialisée par la largeur de l’intervalle de confiance autour de 
