En 1995, le WG1 du JCGM publie le document JCGM 100, « Guide pour l’expression de l’incertitude de mesure », document révisé en 2008 pour des corrections mineures. Il est devenu la norme NF ISO/IEC Guide 98-3 en 2014. Ce document marque une étape importante dans la cadre de l’évaluation des incertitudes de mesure. La méthode qu’il propose, basée sur des propriétés statistiques et mathématiques simples (additivité des variances et loi de propagation), a rapidement été adoptée dans le monde entier et se présente encore de nos jours comme la méthode de référence.
En 2008, le WG1 du JCGM publie le document JCGM 101 « Evaluation of measurement data — Supplement 1 to the “Guide to the expression of uncertainty in measurement” — Propagation of distributions using a Monte Carlo method ». Ce document devient à son tour rapidement une norme internationale (ISO/IEC Guide 98-3 : 2008/SUPPL 1:2008) et présente une alternative à la loi de propagation des incertitudes au cœur du GUM initial. En effet, et comme nous le verrons, la loi de propagation pose un problème dans le cas des modèles de mesure non linéaires, problème que la simulation de Monte-Carlo permet de résoudre.
Même si le GUM est devenu une référence reconnue internationalement pour l’évaluation des incertitudes de mesure, on peut s’accorder sur le fait qu’il est singulièrement compliqué. Les raisons de son manque de pédagogie tiennent sûrement au fait qu’il cherche à traiter en même temps tous les domaines (chimie, électricité, dimensionnel…) et qu’il s’adresse de la même façon à des industriels et à des chercheurs. Par ailleurs, le GUM mélange la justification mathématique (nécessaire évidemment) et la mise en application.
Il propose, préalablement à tout calcul, d’exprimer mathématiquement la relation entre le mesurande Y et les grandeurs d’entrée Xi dont Y dépend (cf. alinéa 1 du § 8 du GUM). Il s’agit là de modéliser le processus de mesure et cette exigence de modélisation a parfois conduit les métrologues voulant respecter le GUM « à la lettre » à certaines acrobaties, notamment lorsqu’il s’agit de mesurer directement une entité. Près de 30 ans de pratiques permettent désormais d’éclaircir ce sujet, notamment en distinguant deux contextes très différents pour l’estimation des incertitudes de mesure, ce que le GUM ne fait pas formellement.
En effet, il se passe des choses très différentes lorsque l’on accède à la valeur recherchée directement par une mesure (le diamètre d’un axe avec un micromètre) ou lorsque l’on y accède en réalisant des mesures directes de différentes grandeurs pour, ensuite, calculer la grandeur d’intérêt (par exemple, la surface d’un échantillon rectangulaire en mesurant sa longueur et sa largeur). Cette différenciation s’avère pourtant extrêmement importante, car ces deux situations ne font pas appel aux mêmes compétences.
Le modèle de mesure
Le premier contexte de mesure est celui dans lequel nous mesurons directement une entité. Plus concrètement, une mesure directe suppose que l’instrument de mesure indique directement la valeur Y du mesurande. Pour autant, cette valeur mesurée Y n’est pas rigoureusement égale à la valeur recherchée, car toute mesure met en jeu différents facteurs imparfaits, tels que rappelés dans la figure ci-après.
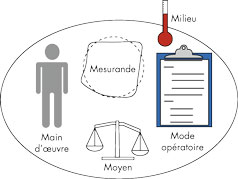
Synoptique d’un processus de mesure
Nous appellerons « modèle de mesure » le modèle qui décrit cette situation de mesure directe. Chacun des facteurs contribuant à la réalisation de la mesure apporte sa propre imperfection au résultat et on peut donc écrire :
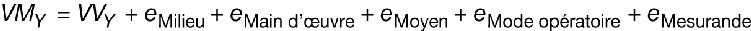
Où :
- VMY : la valeur mesurée du mesurande Y ;
- VVY : la valeur vraie du mesurande Y ;
- eMilieu : l’erreur produite du fait de l’imperfection des conditions environnementales lors de la mesure du mesurande Y ;
- eMain d’œuvre : l’erreur produite du fait de l’imperfection des opérateurs lors de la mesure du mesurande Y ;
- eMoyen : l’erreur produite du fait de l’imperfection de l’instrument de mesure utilisé pour la mesure du mesurande Y ;
- eMode opératoire : l’erreur produite du fait de l’impact du mode opératoire mis en œuvre pour la mesure du mesurande Y ;
- eMesurande : l’erreur liée à l’imperfection du mesurande Y lui-même de sa mesure.
Le modèle de mesure est donc un modèle strictement linéaire dans lequel s’ajoutent algébriquement les erreurs élémentaires produites par chacun des facteurs en présence au moment de chaque mesure. Les statisticiens démontrent que, sous certaines conditions, cette somme d’erreurs provenant de facteurs aléatoires régis chacun par une loi de probabilité dont il est possible de déterminer l’espérance et la variance, suit une loi normale d’espérance égale à la somme des espérances et de variance égale à la somme des variances (dans le cas où tous les facteurs sont indépendants, cf. Les outils statistiques qu’il faut connaître et comprendre en métrologie).
Dans le cadre d’un modèle de mesure, l’évaluation de l’incertitude repose sur l’identification des facteurs influents du processus de mesure, la détermination de leur valeur moyenne et la détermination de leur variance. Pour l’estimation des variances, le GUM propose deux méthodes complémentaires.
- les évaluations de type A lorsque nous disposons de données dans lesquelles le facteur en cours d’étude a varié : il s’agit alors simplement de calculer l’écart-type après s’être assuré que la série de données ne comportait pas de valeurs aberrantes et qu’elles étaient effectivement indépendantes ;
- lorsque nous ne disposons pas de données, le GUM propose une évaluation de type B : il s’agit alors d’estimer l’étendue des erreurs possibles liées au facteur analysé et de leur attribuer une loi de probabilité de façon à transformer l’étendue en un objet similaire à un écart-type (appelé « l’incertitude-type ») puisque ce sont les écarts-types au carré (c’est-à-dire les variances) que nous allons ensuite additionner.
Notons que le GUM traite avec un peu de légèreté la question des moyennes, c’est-à-dire des effets systématiques. Il considère qu’ils doivent être corrigés, sans beaucoup plus de précisions. Le lecteur devra donc être attentif, soit à corriger effectivement les effets systématiques, soit à les considérer dans l’expression de l’incertitude dont l’espérance devient alors la somme des espérances des facteurs non corrigés.
A noter
La moyenne algébrique est un estimateur non biaisé de l’espérance mathématique d’une loi de probabilité.
En outre, il est toujours possible que des effets interfèrent avec certains facteurs du processus de mesure, par exemple si la température impacte le mesurande et, en même temps, l’instrument de mesure. Nous sommes alors face à ce que les statisticiens appellent des covariances (des effets qui varient ensemble) et ces covariances modifient parfois de façon importante la loi de probabilité de la somme des erreurs élémentaires qui composent l’erreur de mesure. La covariance est parfois estimée via un coefficient de corrélation, coefficient généralement noté r qui varie entre -1 et +1 et exprime la force et le sens de la relation entre deux variables. Lorsqu’il vaut 0, les variables sont indépendantes, lorsqu’il vaut -1, elles sont totalement liées et varient en sens opposé et pour +1, elles sont également totalement liées mais varient dans le même sens.
Le modèle de mesure, tel que décrit ci-dessus, s’inscrit résolument dans le monde de la physique. Pour évaluer les incertitudes, il faut donc comprendre les phénomènes physiques qui entrent en jeu dans la réalisation de la mesure, identifier ceux qui la perturbent, évaluer leurs paramètres descriptifs (moyenne et écart-type) et envisager les corrélations qui, elles aussi, sont directement l’expression de phénomènes physiques.
L’incertitude de mesure « en pratique »
Lorsque ces concepts finalement simples sont assimilés, il est possible de proposer une définition très descriptive de ce qu’est, au fond, l’incertitude de mesure. Le VIM lui donne une définition absconse (cf. définition 2.26) alors que quelques mots suffisent à la décrire de façon univoque : « incertitude de mesure : loi de probabilité des erreurs de mesure ».
Quand tout se passe bien, cette loi de probabilité qui décrit les erreurs de mesure possibles est une loi normale de moyenne nulle (si les effets systématiques de toutes les sources d’erreurs sont corrigés) et de variance égale à la somme des variances qui la compose (+ des termes liés aux covariances s’il en existe). Si les effets systématiques ne sont pas corrigés, l’incertitude de mesure a une moyenne différente de zéro. S’il existe des covariances entre les facteurs, ou si un facteur est largement prédominant sur les autres, la loi pourra ne pas être normale. La simulation numérique peut nous permettre d’observer cette loi de probabilité des erreurs de mesure dans un contexte de modèle de mesure même si, à l’origine, elle n’a pas été envisagée pour cela (cf. Étape « Simuler un modèle de mesure »).
A noter
Il est d’usage de définir l’incertitude-type comme étant l’écart-type de cette loi de probabilité qui résulte de l’ensemble des facteurs qui participent à la réalisation d’une mesure.
Le modèle d’intérêt
Le second contexte de mesure est celui dans lequel nous accédons à la valeur Y du mesurande directement. Il est en effet fréquent que Y soit déterminé par une relation mathématique qui fait appel à plusieurs grandeurs, certaines étant mesurées (et subissant ainsi les problèmes d’incertitude évoqués ci-dessus), d’autres publiées par des organismes internationaux (par exemple, le CODATA), d’autres encore accessibles via des informations spécifiques (données fournisseur, par exemple). Mais les données d’entrée de cette relation, quelle que soit leur origine, sont le plus souvent entachées d’incertitude…
L’évaluation de l’incertitude sur la grandeur d’intérêt Y nécessite alors de propager les incertitudes entachant les données d’entrée (les xi) via le modèle qui les relie à Y, modèle qui peut être, soit une fonction mathématique, soit un algorithme qui agit souvent comme une boîte noire.
Dans le cas d’un modèle mathématique de la forme Y = f(x1, x2,…, xn), le GUM propose une solution pour propager l’incertitude sur les xi dans Y : la loi de propagation des incertitudes. Lorsque la fonction f est linéaire sur la plage d’incertitude de chacun des xi, il est possible d’approximer ladite fonction par sa tangente autour des xi et la propagation des incertitudes sur les xi dans Y s’écrit alors, s’il n’y a pas de covariance entre les données d’entrée :
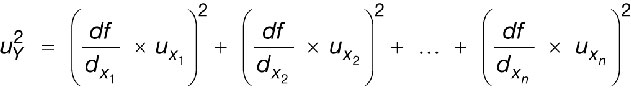
Où :
-
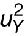 : le carré de l’incertitude-type sur Y (c’est-à-dire la variance associée au résultat Y) ;
: le carré de l’incertitude-type sur Y (c’est-à-dire la variance associée au résultat Y) ; -
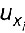 : l’incertitude-type sur la donnée xi ;
: l’incertitude-type sur la donnée xi ; -
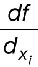 : la dérivée partielle de la fonction f au point xi. Ce facteur est appelé « coefficient de sensibilité » de la donnée d’entrée xi.
: la dérivée partielle de la fonction f au point xi. Ce facteur est appelé « coefficient de sensibilité » de la donnée d’entrée xi.
A noter
Dans le cas d’un algorithme « boîte noire », les dérivées partielles ne sont pas calculables directement, mais il est possible de les estimer numériquement.
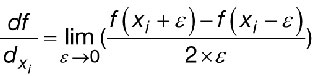
A noter
Comme cette estimation tient compte de toutes les valeurs d’entrée xi de la relation, il faut réestimer cette valeur à chaque fois que l’un au moins des xi change de valeur…
Cas des covariances
Lorsqu’il existe des covariances entre les données d’entrée, il convient d’ajouter à la valeur 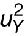 calculée ci-dessus les termes liés aux dites covariances :
calculée ci-dessus les termes liés aux dites covariances :
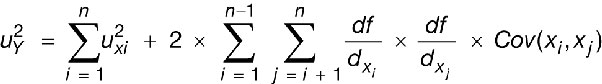
Où :
Cov(xi, xj) : la covariance entre xi et xj.
A noter
Lorsque la covariance est estimée via un coefficient de corrélation, on rappelle : 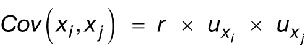
Il est d’usage, dans le cas des modèles d’intérêt, de présenter les données d’entrée sous la forme d’un vecteur de valeurs ( 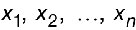 ) qui représente les valeurs numériques permettant de calculer Y et une matrice de variances/covariances, ou une matrice « mixte », qui permet d’exprimer les variances sur les données d’entrée dans la diagonale et, soit les covariances, soit les coefficients de corrélation, dans les termes non diagonaux.
) qui représente les valeurs numériques permettant de calculer Y et une matrice de variances/covariances, ou une matrice « mixte », qui permet d’exprimer les variances sur les données d’entrée dans la diagonale et, soit les covariances, soit les coefficients de corrélation, dans les termes non diagonaux.
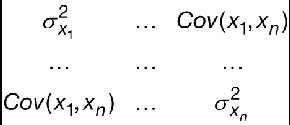
Forme d’une matrice de variances/covariances
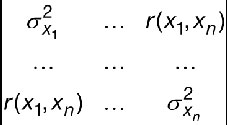
Forme d’une matrice mixte
La loi de propagation des incertitudes proposée par le GUM s’appuie sur le théorème de Taylor. Il s’agit d’approximer la fonction
f au voisinage des points
xi en fonction de ses dérivées aux ordres 1, 2, …
n (sous réserve que la fonction soit dérivable
n fois). Le GUM limite cette approximation à l’ordre 1 mais il peut être nécessaire d’aller plus loin dans les cas où la linéarité au voisinage des
xi n’est pas garantie, ce qui peut rapidement compliquer les calculs de
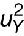
.
D’autre part, rien ne garantit que le résultat de la propagation de toutes les incertitudes sur les données d’entrée conduise à une loi normale. De ce fait, l’estimation de la variance résultante ne permet pas d’attribuer un niveau de confiance effectif à l’incertitude finale puisque la relation 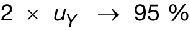 de probabilité ne vaut que si la loi est gaussienne. Autrement dit, à quoi peut bien servir uY si l’on ne connaît pas la nature de la loi de probabilité dont il estime l’écart-type ?
de probabilité ne vaut que si la loi est gaussienne. Autrement dit, à quoi peut bien servir uY si l’on ne connaît pas la nature de la loi de probabilité dont il estime l’écart-type ?
A noter
Il est d’usage, dans de nombreux domaines, d’exprimer l’incertitude sur une valeur Y par un intervalle de confiance établi pour un niveau de confiance égal à 95 %, soit un intervalle d’étendue 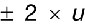 dans le cas d’une incertitude de mesure suivant une loi normale (cas présumé par le GUM).
dans le cas d’une incertitude de mesure suivant une loi normale (cas présumé par le GUM).
Contrairement au modèle de mesure tel que décrit ci-avant, le modèle d’intérêt se situe exclusivement sur un domaine « mathématique ». Le modèle de mesure relève du monde physique, comme expliqué ci-dessus, tandis que la propagation de ce qui s’y passe relève de compétences plus théoriques. Ainsi, le métrologue a une double casquette, mais il est toujours possible de distinguer les profils. Certains ont plus d’appétence pour les manipulations (mesures directes), d’autres pour les exercices plus théoriques (modèle d’intérêt). Dans les deux cas, la pratique d’une métrologie orientée « incertitude » offre, comme nous venons de le voir, de nombreuses perspectives.











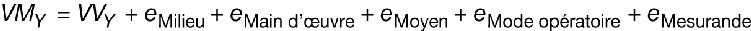
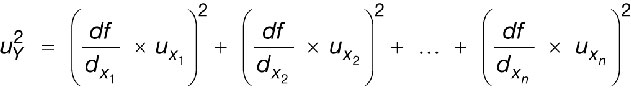
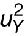 : le carré de l’incertitude-type sur Y (c’est-à-dire la variance associée au résultat Y) ;
: le carré de l’incertitude-type sur Y (c’est-à-dire la variance associée au résultat Y) ;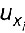 : l’incertitude-type sur la donnée xi ;
: l’incertitude-type sur la donnée xi ;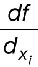 : la dérivée partielle de la fonction f au point xi. Ce facteur est appelé « coefficient de sensibilité » de la donnée d’entrée xi.
: la dérivée partielle de la fonction f au point xi. Ce facteur est appelé « coefficient de sensibilité » de la donnée d’entrée xi.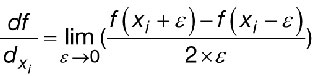
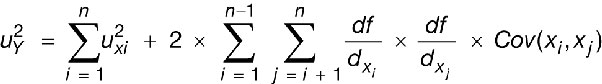
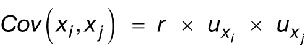
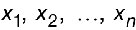 ) qui représente les valeurs numériques permettant de calculer Y et une matrice de variances/covariances, ou une matrice « mixte », qui permet d’exprimer les variances sur les données d’entrée dans la diagonale et, soit les covariances, soit les coefficients de corrélation, dans les termes non diagonaux.
) qui représente les valeurs numériques permettant de calculer Y et une matrice de variances/covariances, ou une matrice « mixte », qui permet d’exprimer les variances sur les données d’entrée dans la diagonale et, soit les covariances, soit les coefficients de corrélation, dans les termes non diagonaux.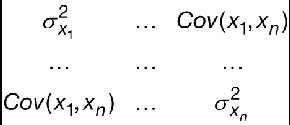
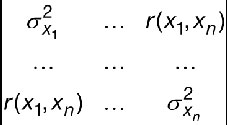
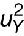 .
. 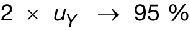 de probabilité ne vaut que si la loi est gaussienne. Autrement dit, à quoi peut bien servir uY si l’on ne connaît pas la nature de la loi de probabilité dont il estime l’écart-type ?
de probabilité ne vaut que si la loi est gaussienne. Autrement dit, à quoi peut bien servir uY si l’on ne connaît pas la nature de la loi de probabilité dont il estime l’écart-type ?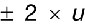 dans le cas d’une incertitude de mesure suivant une loi normale (cas présumé par le GUM).
dans le cas d’une incertitude de mesure suivant une loi normale (cas présumé par le GUM).
